En el fascinante mundo de la geometría, uno de los conceptos más importantes y a menudo ignorados son las rectas notables en triángulos. Estas rectas tienen propiedades únicas y juegan roles cruciales en una serie de teoremas y problemas matemáticos. Si bien puede parecer un tema complejo a primera vista, con un poco de estudio y práctica, se convierte en una herramienta esencial para cualquier estudiante de matemáticas, especialmente aquellos que se preparan para exámenes tanimportantes como el de la UNAM.
Las rectas notables en triángulos son esenciales para entender la estructura y las propiedades de estos polígonos. Estas rectas, que incluyen la mediana, la bisectriz, la altura y la mediatriz, proporcionan información vital sobre el triángulo y contribuyen a la resolución de problemas complejos. Por ejemplo, en un triángulo, las tres medianas se intersectan en un punto llamado baricentro, que es el centro de gravedad del triángulo. Este tipo de conocimientos son fundamentales al enfrentarse a los desafíos matemáticos del examen de la UNAM.
Con la guía adecuada y el estudio constante, las rectas notables en triángulos pueden pasar de ser un concepto abstracto a una valiosa herramienta de resolución de problemas. Ya sea que estés buscando mejorar tus habilidades matemáticas generales o que estés centrado en prepararte para el examen de la UNAM, entender y aplicar estos conceptos puede ser la clave para alcanzar tus metas académicas.
Desentrañando los secretos: Las 4 rectas notables en un triángulo explicadas
En el fascinante mundo de la geometría, a menudo nos encontramos con figuras y formas que nos dejan perplejos. Uno de esos enigmas es el triángulo, una figura que parece simple a primera vista, pero al profundizar en ella, descubrimos características y propiedades asombrosas.

En el vasto mundo de la geometría, los triángulos son una figura fundamental que todos conocemos. Pero, ¿alguna vez te has detenido a pensar cuántas líneas rectas se necesitan para formar un triángulo? A simple vista, la respuesta puede parecer obvia. Sin embargo, hay mucho más en esta pregunta de lo que podrías pensar.
En su forma más básica, un triángulo se compone de tres líneas rectas. Cada una de estas líneas, conocidas en términos técnicos como “segmentos de línea”, se conecta en un punto con las otras dos. Estos puntos de conexión, o “vértices”, son lo que da al triángulo su forma y estructura.
- La primera línea recta puede ser de cualquier longitud y en cualquier dirección. Esta línea inicial es lo que establecerá la base para tu triángulo.
- La segunda línea recta debe comenzar en un extremo de la primera línea y extenderse en cualquier dirección excepto en línea recta. Esta línea establecerá uno de los vértices de tu triángulo.
- La tercera y última línea recta debe comenzar en el extremo abierto de la segunda línea y terminar en el extremo abierto de la primera línea. Esta línea completa el triángulo, formando los dos vértices restantes.
Por lo tanto, la respuesta a la pregunta es que se necesitan tres líneas rectas para formar un triángulo. Pero recuerda, esta es solo la respuesta en su forma más básica. En la geometría, como en muchas otras áreas de la vida, las cosas pueden volverse mucho más complicadas cuando empiezas a considerar diferentes variables y posibilidades.
| Geometría | Líneas rectas necesarias para formar un triángulo |
|---|---|
| En su forma más básica | Tres |
| Con variables y posibilidades | Depende de las condiciones |
Por ejemplo, si estás trabajando en un entorno tridimensional, podrías formar lo que se conoce como un “triángulo esférico” utilizando tres grandes círculos en lugar de líneas rectas. O, si estás trabajando en un plano curvo, podrías necesitar utilizar líneas curvas en lugar de rectas para formar tu triángulo.
Entonces, aunque la respuesta básica es tres líneas rectas, la verdadera respuesta podría ser “depende”. Como en muchas otras cosas en la vida, la verdadera belleza y misterio de la geometría radican en su complejidad y en las infinitas posibilidades que ofrece.
Descubriendo la Mediatriz UNAM: Tu Guía Exhaustiva para Entenderla
La Mediatriz UNAM es un concepto matemático fascinante que a menudo se pasa por alto en los estudios convencionales. Con esta guía, esperamos ayudarte a entenderla mejor y a descubrir su belleza única.
La Mediatriz UNAM se basa en la geometría euclidiana y es una línea recta que divide un segmento en dos partes iguales. Pero, ¿qué la hace tan especial? Bueno, aquí es donde las cosas se ponen interesantes.
- En primer lugar, la Mediatriz UNAM siempre es perpendicular al segmento que divide. Esto significa que forma un ángulo de 90 grados con el segmento.
- En segundo lugar, cada punto en la Mediatriz UNAM es equidistante de los extremos del segmento. Esto hace que sea increíblemente útil en una amplia variedad de aplicaciones matemáticas y científicas.
- Por último, pero no menos importante, la Mediatriz UNAM es simétrica. Si dibujas una línea a través del punto medio del segmento, obtendrás dos mediatrices que se reflejan exactamente una en la otra.
| Característica | Descripción |
|---|---|
| Perpendicularidad | Forma un ángulo de 90 grados con el segmento |
| Equidistancia | Cada punto es equidistante de los extremos del segmento |
| Simetría | Las mediatrices reflejan una en la otra |
Estas características únicas hacen de la Mediatriz UNAM una herramienta valiosa en diversos campos que van desde la física hasta la arquitectura, pasando por la cartografía. Por lo tanto, comprenderla y dominarla no sólo te proporcionará una mayor apreciación de la matemática, sino que también podría abrirte nuevas oportunidades en tu carrera y en tu vida diaria. Así que, ¿a qué esperas? ¡Empieza a descubrir la Mediatriz UNAM hoy mismo!
Desvelando el Misterio: Puntos de Convergencia en Triángulos – Una Guía Completa
En el vasto universo de la geometría y la matemática, los triángulos ocupan un lugar especial. Estas figuras de tres lados pueden parecer simples a primera vista, pero esconden una multitud de secretos y propiedades fascinantes. Un aspecto particularmente intrigante son los puntos de convergencia en triángulos.
Para entender lo que son estos puntos de convergencia y por qué son tan importantes, primero necesitamos entender lo que significa ‘converger’. En términos sencillos, converger se refiere a la tendencia de varias líneas o caminos a encontrarse en un punto común. En el caso de los triángulos, estos puntos de convergencia son lugares donde ciertas líneas dibujadas a través del triángulo se encuentran.
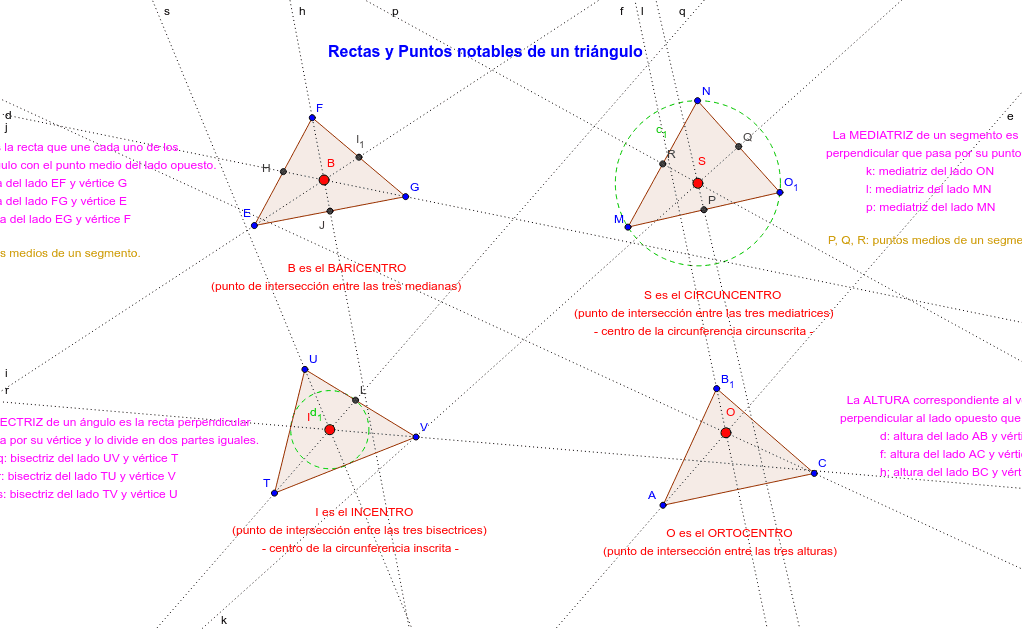
Ahora, uno podría preguntarse, ¿qué líneas son estas?
Bueno, aquí es donde las cosas se ponen realmente interesantes. Existen varios tipos de líneas que podemos trazar en un triángulo, y cada una tiene su propio punto de convergencia. Algunas de las más importantes son:
- Mediatrices: son las perpendiculares trazadas desde el punto medio de cada lado del triángulo. Su punto de convergencia es el circuncentro.
- Alturas: son las perpendiculares trazadas desde cada vértice al lado opuesto. Su punto de convergencia es el ortocentro.
- Bisectrices: son las líneas que dividen cada ángulo en dos partes iguales. Su punto de convergencia es el incentro.
- Medianas: son las líneas trazadas desde cada vértice al punto medio del lado opuesto. Su punto de convergencia es el baricentro.
Ahora, lo que resulta fascinante es que todos estos puntos de convergencia existen siempre, sin importar la forma o tamaño del triángulo. Además, cada uno de estos puntos tiene sus propias propiedades y aplicaciones únicas, lo que hace que los triángulos sean una gran herramienta para explorar una amplia gama de conceptos matemáticos.
| Tipo de Linea | Punto de Convergencia |
|---|---|
| Mediatrices | Circuncentro |
| Alturas | Ortocentro |
| Bisectrices | Incentro |
| Medianas | Baricentro |
Así que la próxima vez que veas un triángulo, recuerda que no es sólo una figura simple. De hecho, es un tesoro de puntos de convergencia, cada uno con su propio conjunto de propiedades y misterios esperando ser descubiertos.

Conclusiones
En resumen, las rectas notables en triángulos son herramientas primordiales para aprovechar y tener éxito en los exámenes de la UNAM. Estos elementos geométricos, que incluyen mediatrices, bisectrices, alturas y medianas, desempeñan un papel crucial en la solución de problemas y en la demostración de teoremas. Su dominio resulta fundamental para explorar nuevas formas de pensamiento lógico y analítico, habilidades imprescindibles para cualquier aspirante a esta prestigiosa universidad.
Por último, recordemos que la comprensión y aplicación de las rectas notables en triángulos no solo es la clave para el examen UNAM, sino que también abre puertas a un mundo de conocimientos matemáticos más amplio. Así que, si te estás preparando para este importante examen, invierte tiempo en familiarizarte con estas rectas notables. Verás cómo tu capacidad para resolver problemas y pensar de manera crítica aumenta, preparándote no solo para el examen, sino para cualquier desafío que pueda presentar tu futura carrera académica.






¿Será que estas rectas notables son la clave para desbloquear el éxito en matemáticas? 🤔
¿Y si las rectas notables en los triángulos son solo un truco matemático? ¡Cuestionemos todo!
¡Las rectas notables en los triángulos son fundamentales en geometría! No son trucos, son conceptos clave. Cuestionar está bien, pero negar su importancia es ignorar la base de la geometría. ¡Vamos a valorar el conocimiento matemático en lugar de desestimarlo!
¿Y si en lugar de rectas notables hablamos de figuras misteriosas en triángulos? 🤔
¿Y si estas rectas notables en triángulos son la clave para dominar el mundo matemático? 🤔